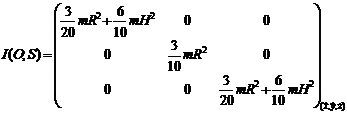MATRICE D’INERTIE…ce qu’il faut connaître

Cas où le solide admet un plan de symétrie matérielle

Cas où le solide admet deux plans de symétrie matérielle

Cas où le solide présente une symétrie de révolution

Cas où le solide présente une épaisseur négligeable (plaque mince)

Moment d’inertie par rapport à un axe quelconque

Théorème de Huygens généralisé

Moments principaux d’inertie et repère principal d’inertie

Matrices d’inertie de quelques solides courants

La masse « m » seule ne permet pas de caractériser la difficulté à mettre un solide en mouvement. Dans le cas particulier où ce mouvement est une translation, la masse suffit, mais pour des mouvements plus complexes, la répartition de cette masse sur le solide est à retenir.

Deux quantités scalaires: le moment d’inertie et le produit d’inertie, caractérisent cette répartition autour d’un axe. Ces deux quantités s’expriment en Kg.m² et nous allons détailler leurs propriétés.

Opérateur d’inertie

On peut synthétiser les notions présentées plus haut dans un opérateur qui est l’opérateur linéaire d’inertie. Appliqué à un vecteur constant dans ,son expression est la suivante:

Cet opérateur est linéaire, donc représentable par une matrice (voir cours de maths).

Dans nos applications, le vecteurs sera le vecteur rotation du solide par rapport à un repère R.

La matrice d’inertie du solide (S) au point O, relativement à la base ,s’obtient en disposant en colonnes les transformés des vecteurs de la base par l’opérateur d’inertie.

en intégrant sur tout le solide :

Les composantes de la matrice d’inertie sont traditionnellement notées :

avec :

A : moment d’inertie du solide par rapport à

B : moment d’inertie du solide par rapport à

C : moment d’inertie du solide par rapport à

D: produit d’inertie par rapport au plan

E: produit d’inertie par rapport au plan

F: produit d’inertie par rapport au plan

Nous allons passer en revue quelques cas particuliers de symétrie rencontrés dans les problèmes.

Cas où le solide admet un plan de symétrie matérielle [haut de page]

P est plan de symétrie matérielle de normale pour le solide.

On peut alors séparer l’intégrale sur (S), en une somme d’intégrales sur (S₁) et (S₂).

On a :

et

Par conséquent :

Cas où le solide admet deux plans de symétrie matérielle [haut de page]

Compte tenu du résultat précédent, si S admet deux plans de symétrie orthogonaux de normales, par exemple, et , alors :

tous les produits d’inertie sont nuls

Cas où le solide présente une symétrie de révolution [haut de page]

Un solide de révolution d’axe , par exemple, admet au moins deux plans de symétrie perpendiculaires, donc les produits d’inertie sont nuls.

Les axes et jouent le même rôle du point de vue géométrique et du point de vue de la répartition des masses, par conséquent les moments d’inertie A et B sont égaux

ce qui est vrai pour toute base contenant .

D’autre part dans ce cas :

le calcul de C ne se fera donc pas directement.

Cas où le solide présente une épaisseur négligeable (plaque mince) [haut de page]

Si l’épaisseur suivant est négligeable devant les autres dimensions alors

Donc E = D = 0 et C = A + B

par conséquent

Généralisation des résultats

Moment d’inertie par rapport à un axe quelconque [haut de page]

Le moment d’inertie I_D d’un solide S par rapport à une droite (A,D) de vecteur unitaire,s’obtient par:

Théorème de Huygens généralisé [haut de page]

Le passage d’une matrice d’inertie définie en G, centre d’inertie de S, à la matrice d’inertie en A s’écrit:

a, b, c étant les coordonnées de G dans le repère lié au solide S.

Moments principaux d’inertie et repère principal d’inertie [haut de page]

La matrice d’inertie est symétrique donc diagonalisable. Les moments principaux sont les valeurs propres de la matrice diagonalisée et la base du repère principal correspond au vecteurs propres associés. Exemples :

ici la base est principale d’inertie